The university where I taught moved classes to zoom in March of 2020. I hated it. I pulled my own grade-school children out of their iPad-classes and homeschooled them in the afternoons in Latin, mathematics, and classical rhetoric.
The pandemic was depressing, but it also sparked hobbies and shaped relationships in new and memorable ways. I started mountain biking, learned how to bake Portuguese custard tarts, recorded music, and planted a vegetable garden with my sons.
One of my favorite Covid memories came in June of 2020. Restless and starved for quality conversation, I purchased an edition of Euclid’s Elements of Geometry and create a group video call with five close friends.
A high school principal, a chef, a media and communications director, a classical humanities teacher, a youth soccer coach, and myself. The six of us in six different places, arrayed across the U.S., on zoom with our editions of Euclid. We discovered a website called GeoGebra that allowed us to sketch diagrams and type out Euclid’s logic.
Each week, we memorized three of his propositions, in order beginning with the first. And then we hopped on Zoom late at night (especially late for the East Coaster), and three of us were chosen at random to reproduce from memory one of the memorized propositions. After the proposition was laid out on GeoGebra, we got “stuck in,” as they say across the pond, questioning and debating the proof’s logic, rhetoric, and philosophical underpinnings. How can he say that? Did he skip a step? Can this be demonstrated empirically? …you’re missing the point! What is a thing that “has no breadth and no length” anyway?
If you’ve read to this point in this post and haven’t studied Euclid before, I wonder what you might be thinking. Euclid is the father of geometry. But this isn’t high school geometry — at least not at most high schools in the 90s when we attended. In fact, arithmetic really has very little to do with it. Poetry, theology, logic, and even aesthetics better characterize the experience of studying Euclid.
Case in point. The second proposition in the first book of the Elements seeks “To place a straight-line equal to a given straight line at a given point (as an extremity).” Essentially, the idea is to prove that if there exists a line (BC), then it is possible to draw a second line (AL) that is the same length as the first.
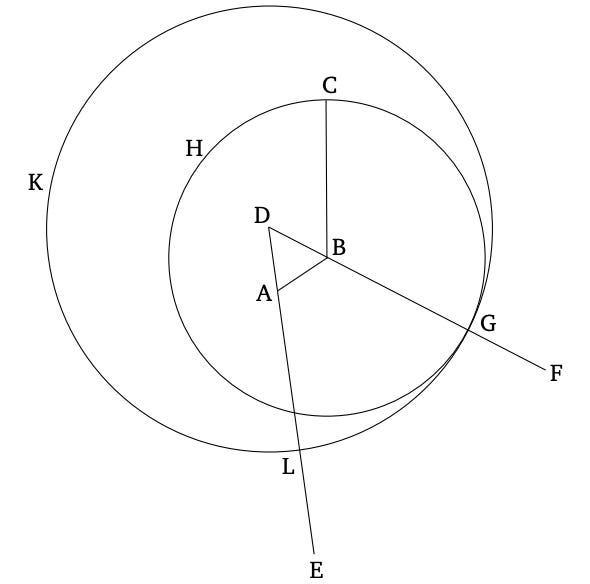
That might seems like a straightforward enough thing to do. Get out your ruler, measure the first line, then draw a second. But that’s not what Euclid is trying to prove. Euclid’s interest is to demonstrate that it is possible, on logical grounds alone, to perform this. Prove that, in theory, I can make an equilateral triangle, or that the sum of two right angles is equal to that of a straight line. Don’t show me. Tell me.
To moderns like us, that should sound awkward. What does it even mean to prove that I can create a line of equal length to another line? Well, it means a great deal. To do this would imply that:
bodies (things) in theory follow regular laws or principles of reason
certain principles (like straightness or equality) are known to us inherently, by virtue of the faculty of reason itself
manmade language can be used to describe truths of equivalency and difference soundly
it’s possible to communicate a truth to another person in a way that carries all of the certainty possessed by the first person
there exists an order in the world, and not only is it reasonable but also impressive, moving, and beautiful
I don’t remember querying those implications of the 3-4-5 triangle in high school. But I do remember feeling deeply challenged. The experience was especially challenging for those members of my discussion group that were teaching in conventional schools.
“What are we even arguing about?.” they would say. “That’s 180 degrees so we know that it’s a straight line.” Of course we do. That’s how we think, two or three times removed from the kind and quality of knowledge that Euclid was aiming for.
“But 180 is just a number that we’ve chosen to represent something we know as straightness,” another would contend. Let’s not be satisfied with the convention we memorized to pass the test. Let’s understand why it’s true.
So there I was, enjoying the California summer evening in my backyard, zooming with five friends, letting Euclid cut away at our unexamined beliefs about reason, equality, language, and beauty.
And yes, I mean beauty. The adjective that first comes to mind when I think of Euclid is “elegant.”
The adjective that first comes to mind when I think of Euclid is “elegant.”
Aristotle begins his work on Poetics by reminding us that one of the fundamental human delights is the experience of learning something. Poetics is about works of art that fit reality, stories that are moving and beautiful — and the principle that reinforces it all is the delight of learning. We take pleasure in seeing something as true, recognizing the equivalence, understanding an explanation. As children we do it with basic acts like simple words (that’s a “chair”) and addition (3 + 2 = 5). Euclid offers this experience to those of us who are past childhood. Comprehending Euclid is like moving from a musical passage of dissonance or tension into its resolution into the founding sentence of its melody.
Geometry is one of the seven classical liberal arts. And it’s in the group of four of them known as the quadrivium, or “four ways,” along with astronomy, arithmetic, and music. The other “three ways” (logic, grammar, rhetoric) are the tools of learning. But geometry and the quadrivium provide the order of thinking. And Euclid re-ordered the way I think.
If you have any friends who are especially well trained in music, then you’ve experienced what I’m talking about. A pianist who has trained for 20 years has the ability to see the world differently than I do. They have this je ne c'est quoi born from an experiential knowledge that can’t be gotten by reading, scrolling, or talking. It’s a knowledge memorized in the fingers and feet. It’s a language that describes reality as no other language can.
I’m a bad musician, so the closest I’ve come to this has been in my study of Euclid.
Comprehending Euclid is like moving from a musical passage of dissonance or tension into its resolution into the founding sentence of its melody.
To those brave and curious souls who want to experience this, I say go for it. The script is easy. Buy a copy of Euclid, or use any number of the free translations that are online. Choose a group of friends. Give yourselves assignments. And begin. Remember to ask the questions that you’re trained not to ask, or even that you’re habituated not to need to ask. Why would I need to ask what a right angle is? I know it’s 95 degrees. Or whether I can make a line of equal length? We have that technology.
Understanding is not measured by what we no longer need to know, but by what we do know.
I joined one of my cofounders, Professor Jeff Tanner (read his bio here), last weekend at The Gathering, a large Christian philanthropy conference in Austin. While at the event, Jeff and I reunited with the friends we made while participating in a year-long accelerator program with Praxis.
If you don’t know Praxis, you should take a moment to familiarize yourself. Praxis is the nation’s leading organization for the furtherance of what they call “redemptive entrepreneurship.” The organization is one of the shining lights of business and organizational support and development. Their portfolio of business and nonprofit organizations represents some of the most innovative, visionary, and passion-filled ventures in the world.
As members of the Praxis nonprofit accelerator, last year, the Hildegard team spent time asking some of the most difficult questions about Christian venture building — not least of which is, what makes them Christian to begin with?
Frankly, Christian higher education does not have the best track record in articulating and practicing the integration of faith and learning. Even though we’ve inherited such a rich tradition from the early middle ages onward of “faith seeking understanding,” the Christian liberal arts tradition, and theology as the “queen of the sciences,” universities still seem to be reinventing the wheel of what they call “faith integration” every ten-or-so years.
In the world of entrepreneurship, Praxis embodies a clear model — albeit a challenging one. They differentiate between exploitative work (using people for one’s own gain) and ethical work (treating others as yourself, non-exploititatively). Most Christian organizations adopt this ethical approach and maybe sprinkle on some theological education. But Praxis takes it a step further, differentiating a “redemptive framework” from a merely ethical one. The redemptive is defined not simply as not exploiting but as creating, blessing, giving, and hoping. A redemptive venture is one that believes in God’s abundance and that adopts the charge to be co-creators with God.
As our time as active members in the accelerator has ended, I want to take a moment to acknowledge Praxis and to express our gratitude to their team and supporters. If you have an audacious startup, one of the best things you could do is to connect with them.




Thank you for my afternoon of memory lane moments. My daughter studied Euclidean geometry as part of a great books series. It reminds me how inadequate my encouragement toward her study was because I was ignorant of its importance in developing thinking as opposed to my “success” in education; the regurgitation of facts from memory. Having become dazed by the successive years the same, I made the mistake of dismissing what required me to think and reason and question effectively. I became an “honor student “ with neither great knowledge or the drive to innovate and create.
I share that to say thank you for your investment in the young men and women of Hildegard. They have an opportunity to be purposeful entrepreneurs because you and your colleagues refused to be lazy minded. You are making disciples of others made in His image realize their worth and potential.